Two Kreutz comets in Secchi images

The first comet was found by Hua Su in LASCO C3 images of 2007 January 31. His first post is from 15:18 UTC, he gave three positions from 09:18 to 10:42 UTC. These were delayed images, I can follow the comet back to 00:18 UTC. Extrapolating backwards it had entered C3 at about January 30 18:00 UTC (but then was too faint to be clearly seen).

When the HI1A images from January 30 were available on February 03, Alan Watson found the comet in the lower right corner of the 18:01 and 20:01 images. Once found, I could follow it back to 08:01 UTC. This is the first HI1a image that shows the comet well, about 16 hours before it appeared in C3 (and 10 hours before it entered C3).

The first comet in HI1A (enlarged two times)
Animation from five images 22:01 to 06:01 UTC (Jan 30/31)

The second comet in HI1A (enlarged two times)
Animation from five images 20:01 to 04:01 UTC (Jan 31/Feb 01)

The second comet was found by Masanori Uchina in LASCO C3 images of 2007 February 01 as his first SOHO comet. His first post is from 14:49 UTC, he gave four positions from 01:42 to 03:18 UTC. These were delayed images, I can follow the comet back to 20:42 UTC (Jan 31). Extrapolating backwards it had entered C3 at about January 31 18:40 UTC (but then was too faint to be clearly seen).

Alan Watson was again the first to report it in HI1A. I could follow the comet from Jan 31 16:01 to Feb 01 04:01 UTC. From these images the first is about 5 hours earlier than the first good C3 image (and only 3 hours before it entered C3).

The second comet was the brighter of the two comets in HI1A and C3, but it became well visible in HI1A later than the first. Both comets showed a steep increase in brightness in HI1A. The first between 10:01 and 12:01 (Jan 30), 19 hours before it left the field. The second between 20:01 and 22:01 (Jan 31), 7 hours before it left the field. The second comet turned on later but became brighter than the first comet.

The first comet entered the COR2 field at about Jan 31 22:00 UTC, about 20 hours after it had entered C3. I found it in the triplets of 00:03 to 02:03 UTC (Feb 01).

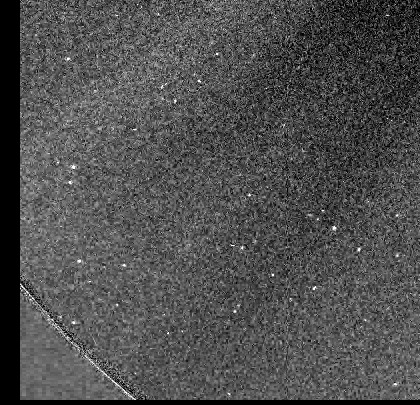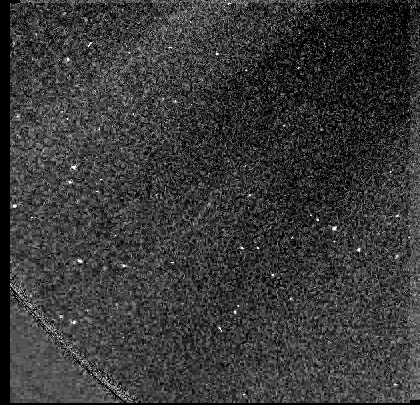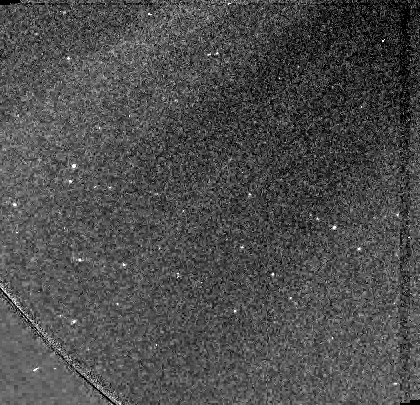
Animation from three triplets 00:03 to 02:03 UTC






















The comet appears rather faint, but with a narrow tail.
One month ago, I have searched for SOHO-1241 in COR2A images. The last image in my COR2A animation shows a very similar object:

triplet from 2006 December 22 02:33
















I think, this is SOHO-1241 (as Alan Watson has suggested earlier).

Rainer Kracht, 2007 February 05

The second Kreutz (found by Masanori Uchina) was also the brighter one in COR2A images

Animation from three triplets 00:03 to 02:03 UTC
(2007 February 02)




















2007 February 07